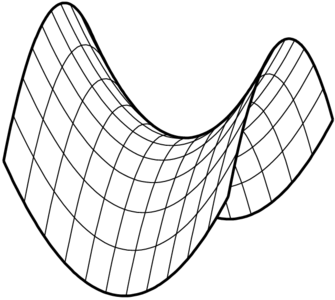
曲面の陰線処理

陰線処理された曲面のワイヤーフレーム表示を行う

主な使用関数: BorderHiddenData, Sf3data, Sfbdparadata, WireHiddenData, Wireparadata.

曲面のプロットデータを得る記法をまとめると、次のようになります:

グラフ型の曲面 $z=f(x,y)\;((x,y)\in[a,b]\times[c,d])$:

fd=list('z=f(x,y)','x=[a,b]','y=[c,d]','ewsn')
(cf. 本稿 — sample:曲面の陰線処理)

領域上のグラフ型の曲面 $z=f(x(u,v),y(u,v))\;((u,v)\in[a,b]\times[c,d])$:

fd=list('z=f(x,y)','x=x(u,v)','y=y(u,v)','u=[a,b]','v=[c,d]','ewsn')
(cf. sample:曲面上の曲線の描画)

パラメータ付けされた曲面 $p(u,v)=(x(u,v), y(u,v), z(u,v))\;((u,v)\in[a,b]\times[c,d])$ :

fd=list('p','x=x(u,v)','y=y(u,v)','z=z(u,v)','u=[a,b]','v=[c,d]',' ')
(cf. sample:パラメータ付けされた曲面の描画)

曲面の描画

視点をSetangle(70,-65)で設定 (tips: 3次元のプロットの視点・投影方向)。曲面 $z=x^2-y^2$ のプロットデータは、fd=list('z=x^2-y^2','x=[-1,1]','y=[-1,1]','ewsn')で得られます。これを(陰線処理されていない)ワイヤーフレーム表示したデータがsurface=Sf3data(fd,50,50)により得られます。

Setangle(70,-65);
Setwindow([-1.5,1.5], [-1.5,1.5]);

fd=list('z=x^2-y^2', 'x=[-1,1]', 'y=[-1,1]', 'ewsn');
surface=Sf3data(fd, 50, 50);

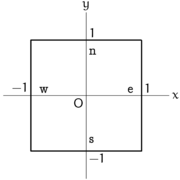fd=list('Z=f(X,Y)','Xの範囲','Yの範囲',境界の指定)で、曲面 $z=f(x,y)$ のプロットデータを指定。他の曲面の指定方法は sample:曲面上の曲線の描画 にて。境界の指定は、ewsnから選んで指定します。

今の場合、右図のように、$\{1\}\times\left[-1,1\right]$が境界'e'にあたり、 $\left[-1,1\right]\times\{1\}$が境界'n'にあたる具合です。逆に、境界がないときは' 'で指定します。この境界の指定が次の輪郭線の表示に関わります。

また、surface=Sf3data(fd,ワイヤーの分割数,曲面のメッシュの分割数)で、陰線処理されていない曲面上のワイヤーのデータが得られます。ここで、ワイヤーの分割数は省略可能で、ワイヤーの折れ線表示の点の個数を表し、デフォルトは50となっています。もしくは、ベクトル[nx,ny]で指定します。曲面のメッシュの分割数も省略可能で、デフォルトで25、x方向y方向で分割数を変えるときは、Nx,Ny のように指定します。

最後に、Windisp(Projpara(surface))でプレビューしてみましょう。ここで、Projpara(surface)で、3次元プロットのデータを2次元のデータに変換(Setangleの値をもとに投影)してます。3次元のプロットデータをWindispでプレビューするために必須です。

Windisp(Projpara(surface));

[このページのトップへ]

陰線処理されたワイヤーフレームと輪郭線

KETpic特有の機能として、曲面の輪郭線のデータを計算するコマンドが用意されています。

outline=Sfbdparadata(fd, 100);

構文はSfbdparadata(fd,分割数)となります。分割数は省略可能で、デフォルトで50=[50,50]。ただし、上で境界として指定しなかった部分は、輪郭線に含まれません。また、これは陰線処理されたデータで、曲面に隠された部分のデータは

houtline=BorderHiddenData();

で得られます。TeXに出力する段階で、Dashline(houtline, 0.5)などと、利用します。

また、陰線処理された曲面上のワイヤーのデータを

wire=Wireparadata(outline, fd, 10, 10);

で得ることができます。構文はWireparadata(outline,fd,横のワイヤーの本数,縦のワイヤーの本数)。また、曲面に隠された部分のデータは、WireHiddenData()で得られます。

[このページのトップへ]

TeXファイルの書き出し

現在のsceファイルのあるディレクトリの下のtexディレクトリにTeXファイルを書き出し。

Openfile('tex/surface_sample1_1.tex');
Beginpicture('1.5cm');
Drwline(Projpara(outline), 1.5);
Drwline(Projpara(wire), 0.5);
Endpicture(0);
Closefile();

Openfile('tex/surface_sample1_2.tex');
Beginpicture('1.5cm');
Drwline(Projpara(outline), 1.5);
Setpen(0.5);
Dashline(Projpara(houtline), 1, 0.5);
Endpicture(0);
Closefile();

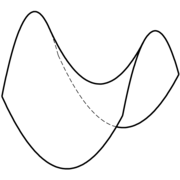前者は(陰線処理された)曲面のワイヤーフレーム表示で、後者は輪郭線の陰線を破線で描画しています(右図)。
Dashline(曲線のデータ,実線の長さ,ギャップの長さ)で破線を描画。破線の太さは、Setpen(0.5)で指定することに注意しましょう。

[このページのトップへ]

ソースコード

scilabファイル(.sce)のダウンロード

tic();

Setangle(70,-65);
Setwindow([-1.5,1.5], [-1.5,1.5]);

fd=list('z=x^2-y^2', 'x=[-1,1]', 'y=[-1,1]', 'ewsn');
surface=Sf3data(fd, 50, 50);

Windisp(Projpara(surface));

outline=Sfbdparadata(fd, 100);
houtline=BorderHiddenData();
wire=Wireparadata(outline, fd, 10, 10);

Windisp(Projpara(outline));
Windisp(Projpara(wire));


Openfile('tex/surface_sample1_1.tex');
Beginpicture('1.5cm');
Drwline(Projpara(outline), 1.5);
Drwline(Projpara(wire), 0.5);
Endpicture(0);
Closefile();

Openfile('tex/surface_sample1_2.tex');
Beginpicture('1.5cm');
Drwline(Projpara(outline), 1.5);
Setpen(0.5);
Dashline(Projpara(houtline), 1, 0.5);
Endpicture(0);
Closefile();

T=toc();  //一番初めのtic();とセットで使って、実行時間を計ります
minute=floor(T/60);
second=floor(T-60*minute);
disp(strcat([string(minute), ' minutes ', string(second), ' seconds']));

自分の環境では、実行するのに3分半ほどかかりました。最後の実行時間を計るコードについては、実行にかかる時間を計るを参照してください。

[このページのトップへ]